Question

PLEASE help me with this question! No nonsense answers and answer with full solutions please!

Answer 1

Answer: b) {-3, 0.5}

Explanation:

The new equation is the original equation plus 6. Move the original graph UP 6 units. The solutions are where it crosses the x-axis.

`\text{Original equation:}\quad f(x)=(15)/(x)-(9)/(x^2)\\\\\\\text{New equation:}\quad(15)/(x)+6=(9)/(x^2)\\\\\\.\qquad \qquad f(x)= (15)/(x)-(9)/(x^2)+6`

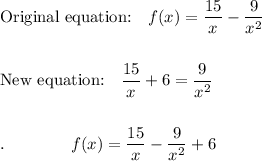
+6 means it is a transformation UP 6 units.

Solutions are where it crosses the x-axis.

The curve now crosses the x-axis at x = -3 and x = 0.5.