Question

Iv)
6x+3y=6xy
2x + 4y= 5xy​

Answer 1

Ok, we have a system of equations:

6*x + 3*y = 6*x*y

2*x + 4*y = 5*x*y

First, we want to isolate one of the variables,

As we have almost the same expression (x*y) in the right side of both equations, we can see the quotient between the two equations:

(6*x + 3*y)/(2*x + 4*y) = 6/5

now we isolate one off the variables:

6*x + 3*y = (6/5)*(2*x + 4*y) = (12/5)*x + (24/5)*y

x*(6 - 12/5) = y*(24/5 - 3)

x = y*(24/5 - 3)/(6 - 12/5) = 0.5*y

Now we can replace it in the first equation:

6*x + 3*y = 6*x*y

6*(0.5*y) + 3*y = 6*(0.5*y)*y

3*y + 3*y = 3*y^2

3*y^2 - 6*y = 0

Now we can find the solutions of that quadratic equation as:

`y = (6 +- √((-6)^2 - 4*3*0) )/(2*3) = (6 +- 6)/(6)`

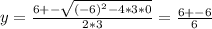
So we have two solutions

y = 0

y = 2.

Suppose that we select the solution y = 0

Then, using one of the equations we can find the value of x:

2*x + 4*0 = 5*x*0

2*x = 0

x = 0

(0, 0) is a solution

if we select the other solution, y = 2.

2*x + 4*2 = 5*x*2

2*x + 8 = 10*x

8 = (10 - 2)*x = 8x

x = 1.

(1, 2) is other solution