Question

The coefficient of x^ky^n-k in the expansion of (x+y)^n equals (nk). True or false.

Answer 1

True

Explanation:

apec

Answer 2

The correct option is;

False

Explanation:

The coefficient of x^k·y^(n-k) is nk, False

The kth coefficient of the binomial expansion, (x + y)ⁿ is
`\dbinom{n}{k} = (n!)/(k!\cdot (n-k)!) = C(n,k)`

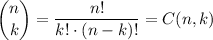
Where;

k = r - 1

r = The term in the series

For an example the expansion of (x + y)⁵, we have;

(x + y)⁵ = x⁵ + 5·x⁴·y + 10·x³·y² + 10·x²·y³ + 5·x·y⁴ + y⁵

The third term, (k = 3) coefficient is 10 while n×k = 3×5 = 15

Therefore, the coefficient of x^k·y^(n-k) for the expansion (x + y)ⁿ =
`C(n,k)` not nk