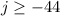Question

Solve the inequality -2/11 j _< 8

Answer 1

`j\geq -44`

Explanation:

The inequality given is:

`(-2)/(11)j\leq 8`

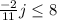
To solve the inequality, we must get the variable j by itself.

j is being multiplied by -2/11. To reverse this, we must multiply by the reciprocal of the fraction.

Flip the numerator (top number) and denominator (bottom number) to find the reciprocal.

`(-2)/(11) --> (-11)/(2)`

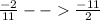
Multiply both sides of the equation by -11/2.

`(-11)/(2) *(-2)/(11) j \leq 8*(-11)/(2)`

`j\leq 8*(-11)/(2)`

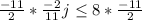
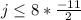
Since we multiplied by a negative number, we must flip the inequality sign.

`j\geq 8*(-11)/(2)`

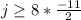
Multiply 8 and -11/2

`j\geq 8*-5.5`

`j\geq -44`

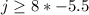
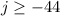
The solution to the inequality is:
`j\geq -44`

Answer 2

j ≥ -44

Explanation:

-2/11 j ≤ 8

Multiply each side by -11/2 to isolate j. Flip the inequality since we are multiplying by a negative

-11/2 * -11/2 j ≥ 8 * -11/2

j ≥ -44