Question

How many real roots and how many complex roots exist for the polynomial

F(x) - X4+ x2 - 5x2 + x -- 6?
O A. 2 real roots and 2 complex roots
B. O real roots and 4 complex roots
O c. 3 real roots and 1 complex root
D. 4 real roots and 0 complex roots

Answer 1

D. 4 real roots and 0 complex roots

Explanation:

If I assume that the function you are saying is

`F(x)=x^4+x^3-5x^2+x-6`

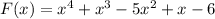
There should be up to "4 roots," there can't be more or less than 4 total solutions. First, we need to check how many sign changes are there in this function. There are 3 positive real roots. Now lets check for negative roots.

`F(-x)=x^4-x^3-5x^2-x-6`

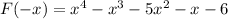
There are is only 1 negative real root. Since we basically have 4 real roots, and the max is 4. There should be 4 real roots and 0 complex roots.