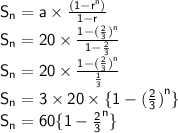(i)

(ii)
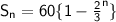
Explanation:

height of ball (a) = 10m
fraction of height decreases by each bounce (r) = 2/3
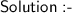
(i) We will use here geometric progression formula to find height an times

(ii) here we will use the sum formula of geometric progression for finding the total nth impact