Question

A particular geometric sequence has strictly decreasing terms. After the first term, each successive term is calculated by multiplying the previous term by $\frac{m}{7}$. If the first term of the sequence is positive, how many possible integer values are there for $m$?

Answer 1

6 possible integers

Explanation:

Given

A decreasing geometric sequence

`Ratio = (m)/(7)`

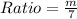
Required

Determine the possible integer values of m

Assume the first term of the sequence to be positive integer x;

The next sequence will be
`x * (m)/(7)`

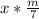
The next will be;
`x * ((m)/(7))^2`

The nth term will be
`x * ((m)/(7))^(n-1)`

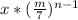
For each of the successive terms to be less than the previous term;

then
`(m)/(7)` must be a proper fraction;

This implies that:

`0 < m < 7`

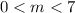
Where 7 is the denominator

The sets of
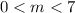`0 < m < 7` is
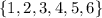`\{1,2,3,4,5,6\}` and their are 6 items in this set

Hence, there are 6 possible integer