Answer:
 .
.
Explanation:
It is given that a candle maker prices one set of scented candles at $10 and sells an average of 200 sets each week.

If he reduces the price by $1,then he sells 50 more candle sets each week.
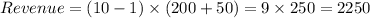
If he reduces the price by x $1,then he sells 50x more candle sets each week.
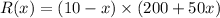
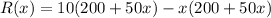
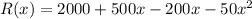
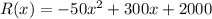
It can be written as

Therefore, the situation can be modeled by the equation
 .
.