Question

Solve the system of equations algebraically.

{Y=(x-2)^2+2
{Y+4=3x

Answer 1

`\large \boxed{\sf \bf \ \text{ The solutions are } x=2, y=2 \text{ and } x=5, y=11.} \ \ }`

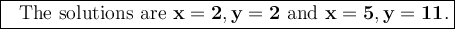
Explanation:

Hello, please consider the following.

We want to solve this system of equations.

`\begin{cases}&y=(x-2)^2+2\\&y+4=3x\end{cases}`

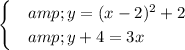
This is equivalent to (subtract 4 from the second equation).

`\begin{cases}&y=(x-2)^2+2\\&y=3x-4\end{cases}`

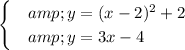
Then, we can write y = y, meaning:

`(x-2)^2+2=3x-4\\\\\text{*** We develop the left side. ***}\\\\x^2-4x+4+2=3x-4 \\\\\text{*** We simplify. *** }\\\\x^2-4x+6=3x-4\\\\\text{*** We subtract 3x-4 from both sides. ***}\\\\x^2-4x+6-3x+4=0\\\\\text{*** We simplify. *** }\\\\x^2-7x+10=0`

`\text{*** The sum of the zeroes is 7 and the product 10 = 5 x 2 ***}\\\\\text{*** We can factorise. ***}\\\\x^2-5x-2x+10=x(x-5)-2(x-5)=(x-2)(x-5)=0\\\\x-2 = 0 \ \ or \ \ x-5 = 0\\\\x= 2 \ \ or \ \ x=5`

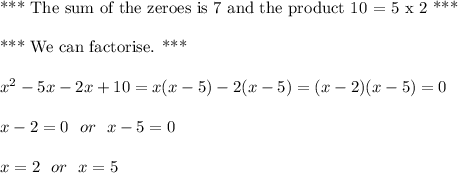
For x = 2, y =0+2=2 (from the first equation) and for x = 5 y=3*5-4=15-4=11 (from the second equation)

So the solutions are (2,2) and (5,11)

Hope this helps.

Do not hesitate if you need further explanation.

Thank you

Answer 2

(5, 11) and (2, 2)

Explanation:

y = (x-2)² + 2

y + 4 = 3x

(x-2)² + 2 + 4 = 3x

x² - 4x + 4 + 6 = 3x

x² - 7x + 10 = 0

(x - 5)(x - 2) = 0

x - 5 = 0, x = 5

x - 2 = 0, x = 2

y = (5-2)² + 2 = 11

(5, 11)

y = (2-2)² + 2 = 2

(2, 2)