Answer:
D
Explanation:
Hello, This is a geometric sequence where the first term is
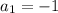 .
.
It means that the sequence is
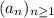 .
.
In other words, as the common ratio is 7 the sequence is defined by
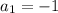
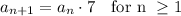
For instance, we can estimate the first terms:
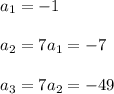
And we know that we can even find a formula for the
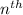 term of the sequence by:
term of the sequence by:
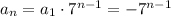
Now, to answer the question, the domain for n is all integers where
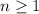 .
.
Hope this helps.
Do not hesitate if you need further explanation.
Thank you