Question

A line passes through the points (-3,1) and (9,5) and is labeled line d. Construct two lines: A line that is parallel to the line d described above through the point (6,7) and is labeled line g A line that is perpendicular to line g through the point (-3,-3) and is labeled line f. What is the equation for line g?

I really need help with this because I'm struggling

Answer 1

The equation of line g is y = x/3 + 5

Explanation:

Given that the line d passes through the points (-3, 1) and (9, 5) we have the equation of line d in slope and intercept form., y = m·x + c found as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

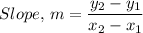
Where;

(x₁, y₁) = (-3, 1)

(x₂, y₂) = (9, 5)

`Slope, \, m =(5-1)/(9-(-3)) = (4)/(12) = (1)/(3)`

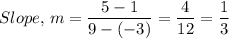
The line, d, in point-slope form is y - 1 = 1/3(x - (-3))

Which gives;

y - 1 = 1/3·x + 3/3

y = 1/3·x + 1 + 1 = 1/3·x + 2

Given that line g is parallel to line d, we have;

Slope of line g = slope of line d = 1/3

Therefore, the equation of line g passing through point ^6, 7) in point-slope form is y - 7 = 1/3(x - 6) which gives;

y = x/3 - 2 + 7 = x/3 + 5

The equation of line g is y = x/3 + 5

The line f passing through point (-3, -3) is perpendicular to ling g, therefore, the slope = -1/m = -1(1/3) = -3

The point-slope form of the equation is y -(-3) = -3(x - (-3)) which gives;

y + 3 = -3·x - 9

Therefore, the equation of line f is y = -3·x - 9 - 3 = -3·x - 12

The equation of line f is y = -3·x - 12.