Question

Simplify
`$(2\sqrt[3]9)/(1 + \sqrt[3]3 + \sqrt[3]9).$` $\frac{2\sqrt[3]9}{1 + \sqrt[3]3 + \sqrt[3]9}.$

Answer 1

`3 -\sqrt[2]3`

Explanation:

Given

`\frac{2\sqrt[3]{9}}{1 + \sqrt[3]{3} + \sqrt[3]{9}}`

Required

Simplify

Rewrite the given expression in index form

`\frac{2 * 9 ^(1)/(3)}{1 + 3^{(1)/(3)} + 9^{(1)/(3)}}`

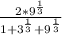
Express 9 as 3²

`\frac{2 * 3^2^*^(1)/(3)}{1 + 3^{(1)/(3)} + 3^2^*^{(1)/(3)}}`

`\frac{2 * 3^(2)/(3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)}}`

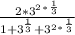
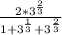
Multiply the numerator and denominator by
`1 - 3^{(1)/(3)}`

`\frac{2 * 3^(2)/(3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)}} * \frac{1 - 3^{(1)/(3)}}{1 - 3^{(1)/(3)}}`

`\frac{2 (3^(2)/(3)) (1 - 3^{(1)/(3)})}{(1 + 3^{(1)/(3)} + 3^{(2)/(3)})(1 - 3^{(1)/(3)})}`

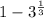
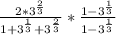
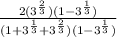
Open the bracket

`\frac{2 (3^(2)/(3)) -2 (3^(2)/(3))(3^{(1)/(3)})}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)}(1 + 3^{(1)/(3)} + 3^{(2)/(3)})}`

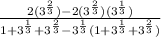
Simplify the Numerator using Laws of Indices

`\frac{2 (3^(2)/(3)) -2 (3^(2+1)/(3))}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)}(1 + 3^{(1)/(3)} + 3^{(2)/(3)})}`

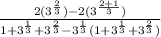
Further Simplify

`\frac{2 (3^(2)/(3)) -2 (3^(3)/(3))}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)}(1 + 3^{(1)/(3)} + 3^{(2)/(3)})}`

`\frac{2 (3^(2)/(3)) -2 (3^1)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)}(1 + 3^{(1)/(3)} + 3^{(2)/(3)})}`

`\frac{2 (3^(2)/(3)) -2 (3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)}(1 + 3^{(1)/(3)} + 3^{(2)/(3)})}`

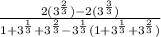
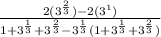
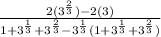
Simplify the denominator

`\frac{2 (3^(2)/(3)) -2 (3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)} - (3^{(1)/(3)})(3^{(1)/(3)}) - (3^{(1)/(3)})(3^{(2)/(3)})}`

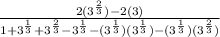
Further Simplify Using Laws of Indices

`\frac{2 (3^(2)/(3)) -2 (3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)} - (3^{(1+1)/(3)}) - (3^{(1+2)/(3)})}`

`\frac{2 (3^(2)/(3)) -2 (3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)} - 3^{(2)/(3)} - 3^{(3)/(3)}}`

`\frac{2 (3^(2)/(3)) -2 (3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)} - 3^{(2)/(3)} - 3^1}}`

`\frac{2 (3^(2)/(3)) -2 (3)}{1 + 3^{(1)/(3)} + 3^{(2)/(3)} - 3^{(1)/(3)} - 3^{(2)/(3)} - 3}}`

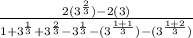
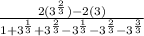
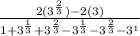
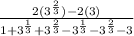
Collect Like Terms

`\frac{2 (3^(2)/(3)) -2 (3)}{1 - 3+ 3^{(1)/(3)} - 3^{(1)/(3)}+ 3^{(2)/(3)} - 3^{(2)/(3)} }}`

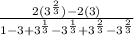
Group Like Terms for Clarity

`\frac{2 (3^(2)/(3)) -2 (3)}{(1 - 3) + (3^{(1)/(3)} - 3^{(1)/(3)}) + (3^{(2)/(3)} - 3^{(2)/(3)} )}}`

`(2 (3^(2)/(3)) -2 (3))/((- 2)+ (0) + (0))}`

`(2 (3^(2)/(3)) -2 (3))/(-2)}`

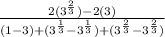
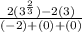
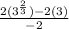
Divide the fraction

`-(3^(2)/(3)) + (3)`

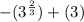
Reorder the above expression

`3 -3^(2)/(3)`

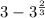
The expression can be represented as

`3 -\sqrt[2]3`

Hence;

`\frac{2\sqrt[3]{9}}{1 + \sqrt[3]{3} + \sqrt[3]{9}}` when simplified is equivalent to
`3 -\sqrt[2]3`