Question

Find the equation of the line that passes through (-1,5) and is perpendicular to y – 5x = 1.

Answer 1

`\huge\boxed{y=-(1)/(5)x+(24)/(5)\to x+5y=24}`

Explanation:

The slope-intercept form of an equation of a line:

`y=mx+b`

m - slope

b - y-intercept

Let

`k:y=m_1x+b_1;\ l:y=m_2x+b_2`

therefore

`k||l\iff m_1=m_2\\k\perp l\iff m_1m_2=-1\to m_2=-(1)/(m_1)`

We have the equation of a line in the standard form. Convert it to the slope-intercept form:

`y-5x=1` add 5x to both sides

`y-5x+5x=1+5x\\\\y=5x+1\to m_1=5;\ b_1=1`

Calculate the slope:

`m_2=-(1)/(5)`

Substitute the value of a slope and the coordinates of the given point (-1, 5) to the equation of a line:

`y=m_2x+b`

`5=\left(-(1)/(5)\right)(-1)+b`

`5=(1)/(5)+b` subtract 1/5 from both sides

`5-(1)/(5)=(1)/(5)-(1)/(5)+b`

`(25)/(5)-(1)/(5)=b\\\\(24)/(5)=b\to b=(24)/(5)`

Final answer:

`y=-(1)/(5)x+(24)/(5)`

convert to the standard form (Ax + By = C):

`y=-(1)/(5)x+(24)/(5)` multiply both sides by 5

`5y=(5)\left(-(1)/(5)x\right)+(5)\left((24)/(5)\right)`

`5y=-x+24` add x to both sides

`x+5y=24`

Answer 2

The answer is

`y = - (1)/(5) x + (24)/(5)`

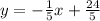
Explanation:

Equation of a line is y = mx + c

where

m is the slope

c is the y intercept

y - 5x = 1

y = 5x + 1

Comparing with the above formula

The slope / m of the line is 5

Since the is perpendicular to y = 5x + 1 it's slope it's the negative inverse of y = 5x + 1

That's

Slope of the perpendicular line = - 1/5

Equation of the line using point (-1,5) is

`y - 5 = - (1)/(5) (x + 1)`

`y - 5 = - (1)/(5) x - (1)/(5)`

`y = - (1)/(5) x - (1)/(5) + 5`

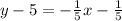
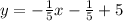
We have the final answer as

`y = - (1)/(5) x + (24)/(5)`

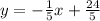
Hope this helps you