Question

A random sample is drawn from a normally distributed population with mean μ = 31 and standard deviation σ = 1.9. Calculate the probabilities that the sample mean is less than 31.6 for both sample sizes

Answer 1

For sample size n = 39 ; P(X < 31.6) = 0.9756

For sample size n = 76 ; P(X < 31.6) = 0.9970

Explanation:

Given that:

population mean μ = 31

standard deviation σ = 1.9

sample mean
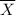`\overline X` = 31.6

Sample size n Probability

39

76

The probabilities that the sample mean is less than 31.6 for both sample size can be computed as follows:

For sample size n = 39

`P(X < 31.6) = P((\overline X - \mu)/((\sigma )/(√(n)))< (\overline X - \mu)/((\sigma )/(√(n))))`

`P(X < 31.6) = P((31.6 - \mu)/((\sigma )/(√(n)))< (31.6 - 31)/((1.9 )/(√(39))))`

`P(X < 31.6) = P(Z< (31.6 - 31)/((1.9 )/(√(39))))`

`P(X < 31.6) = P(Z< (0.6)/((1.9 )/(6.245)))`

`P(X < 31.6) = P(Z< 1.972)`

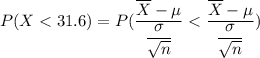
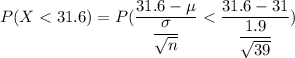
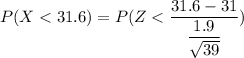
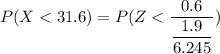
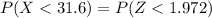
From standard normal tables

P(X < 31.6) = 0.9756

For sample size n = 76

`P(X < 31.6) = P((\overline X - \mu)/((\sigma )/(√(n)))< (\overline X - \mu)/((\sigma )/(√(n))))`

`P(X < 31.6) = P((31.6 - \mu)/((\sigma )/(√(n)))< (31.6 - 31)/((1.9 )/(√(76))))`

`P(X < 31.6) = P(Z< (31.6 - 31)/((1.9 )/(√(76))))`

`P(X < 31.6) = P(Z< (0.6)/((1.9 )/(8.718)))`

`P(X < 31.6) = P(Z< 2.75)`

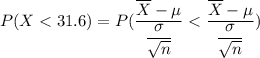
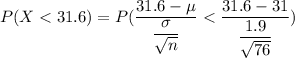
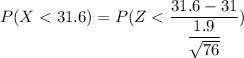
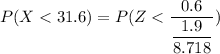
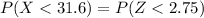
From standard normal tables

P(X < 31.6) = 0.9970