Question

P(x)=2x^5+9x^4+9x^3+3x^2+7x-6;x=i,-2

Answer 1

The value of the polynomial function at P(1) and P(-2) is 24 and 0 respectively.

Explanation:

We are given with the following polynomial function below;

`\text{P}(x) = 2x^(5) +9x^(4) +9x^(3) +3x^(2)+7x-6`

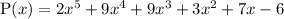
Now, we have to calculate the value of P(x) at x = 1 and x = -2.

For this, we will substitute the value of x in the given polynomial and find it's value.

At x = 1;

`\text{P}(1) = 2(1)^(5) +9(1)^(4) +9(1)^(3) +3(1)^(2)+7(1)-6`

`\text{P}(1) = (2* 1) +(9* 1)+(9 * 1)+(3* 1)+(7* 1)-6`

`\text{P}(1) = 2 +9+9+3+7-6`

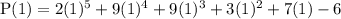
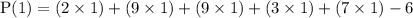
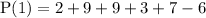
P(1) = 30 - 6

P(1) = 24

At x = -2;

`\text{P}(-2) = 2(-2)^(5) +9(-2)^(4) +9(-2)^(3) +3(-2)^(2)+7(-2)-6`

`\text{P}(-2) = (2* -32) +(9* 16)+(9 * -8)+(3* 4)+(7* -2)-6`

`\text{P}(-2) = -64 +144-72+12-14-6`

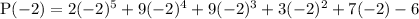
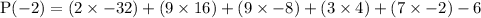
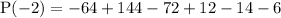
P(-2) = 156 - 156

P(-2) = 0

Hence, the value of the polynomial function at P(1) and P(-2) is 24 and 0 respectively.