Question

4^3/4 x 2^x = 16^2/5
work out the exact value of x

Answer 1

x = 1/10

Explanation:

`{4}^{ (3)/(4) } * {2}^(x) = {16}^{ (2)/(5) }`

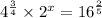
In order to solve the equation express each of the terms in the same base .

in this case we express each of the terms in base 2

That's

`{4}^{ (3)/(4) } = {2}^{2 * (3)/(4) } = {2}^{ (3)/(2) }`

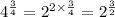
And

`{16}^{ (2)/(5) } = {2}^{4 * (2)/(5) } = {2}^{ (8)/(5) }`

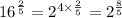
So we have

`{2}^{ (3)/(2) } * {2}^(x) = {2}^{ (8)/(5) }`

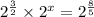
Since the left side are in the same base and are multiplying, we add the exponents

`{2}^{ (3)/(2) + x } = {2}^{ (8)/(5) }`

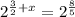
Since they have the same base we can equate them

That's

`(3)/(2) + x = (8)/(5)`

`x = (8)/(5) - (3)/(2)`

`x = (1)/(10)`

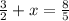
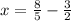
Hope this helps you