Question

A group of patients select from among 38 numbers, with 18 odd numbers (black) and 18 even

numbers (red), as well as 0 and 00 (which are green). If a doctor pays $7 that the outcome is an odd
number, the probability of losing the $7 is 20/38 and the probability of winning $14 (for a net gain of
only $7, given you already paid $7) is 18/38
If a doctor pays $7 that the outcome is an odd number, how would you figure out what is the doctors
expected value is?

Answer 1

Answer: $2.95

Explanation:

Given: Probability of losing the $7 =
`(20)/(38)`

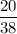
Probability of winning $14 =
`(18)/(38)`

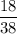
Then, the expected value = (- $7) x ( Probability of losing the $7) + $14 x(Probability of winning $14)

=
`(-\$ 7)*(20)/(38)+(\$14)*(18)/(38)`

=
`-(70)/(19)+(126)/(19)`

=
`(56)/(19)*\approx\$2.95`

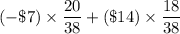
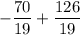
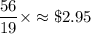
∴ If a doctor pays $7 that the outcome is an odd number, the doctor's

expected value is $2.95.