Question

Construct a 90% confidence interval for the true mean using the FPCF. (Round your answers to 4 decimal places.) The 90% confidence interval is from to

Answer 1

The answer is below

Explanation:

Twenty-five blood samples were selected by taking every seventh blood sample from racks holding 187 blood samples from the morning draw at a medical center. The white blood count (WBC) was measured using a Coulter Counter Model S. The mean WBC was 8.636 with a standard deviation of 3.9265. (a) Construct a 90% confidence interval for the true mean using the FPCF. (Round your answers to 4 decimal places.) The 90% confidence interval is from to

Answer:

Given:

Mean (μ) = 8.636, standard deviation (σ) = 3.9265, Confidence (C) = 90% = 0.9, sample size (n) = 25

α = 1 - C = 1 - 0.9 = 0.1

α/2 = 0.1/2 = 0.05

From the normal distribution table, The z score of α/2 (0.05) corresponds to the z score of 0.45 (0.5 - 0.05) which is 1.645

The margin of error (E) is given by:

`E=z_{(\alpha)/(2) }*(\sigma)/(√(n) )\\ \\E=1.645*(3.9265)/(√(25) )=1.2918`

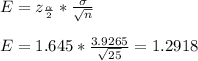
The confidence interval = μ ± E = 8.636 ± 1.2918 = (7.3442, 9.9278)

The 90% confidence interval is from 7.3442 to 9.9278