Answer:
the width of the rectangle is 24 centimeters and the length is 31 centimeters.
Explanation:
We first have to write an equation for this, but let's just recall that the area of a rectangle is equal to the length times the width. A=L×W.
A is the area
L is the length
W is the width.
So, for our equation we can start out by putting that 744= ? times ?.
So, we are given that the length is 7 more than the width. We are going to have to translate that to represent the length.
We need a variable. Let's use the letter "W," the width of the rectangle.
W=W.
The length is 7 more than the width, so it is L=W+7.
Length represents the W+7
Width represents W.
Now, we can complete our equation.
744=W(W+7).
Simplify the expression.
744=
 +7W.
+7W.
Alright, you may be thinking on how we are going to solve this problem. This equation correlates with quadratic functions.
Let's complete the square.
In a quadratic function, the standard from is y=
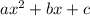 .
.
We need to find the c value.
We can do this by applying a formula. The formula states that c= b/2 and the whole thing squared. In other words,
 .
.
In this case, the b value is 7.
square 7, which is 49 and square 2 which is 4.
Now, the c value is 49/4.
We have now just created a perfect square trinomial.
Not only do we add 49/4 to W squared plus 7W, we also add 49/4 to 744.
744 plus 49/4 is 756/25.
Now, we have

Change W squared plus 7w plus 49/4 to a binomial squared.
Just take the square root of the a value, W, and 49/4 for c. the square root of W squared is W. the square root of 49/4 is 7/2.
Those values are to the power of 2.
In other words,
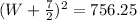
To isolate for W, take the square root of both sides.The square root of W plus 7/2 squared is just W+7/2. The square root of 756.25 is 27.5
There are two solutions for W because square roots be positive or negative, but we are dealing with positive since negative doesn't make sense with the context of the problem.
We have
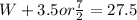
Isolate for W by subtracting both sides by 3.5 You get to W=24.
Therefore, the width of the rectangle is 24 centimeters.
Alright, we found the width. We now need to find the length. The problem stated that the rectangle was 7 more than the width. So, 24+7=31. Therefore, the length of the rectangle is 31 centimeters.
L=31cm
W=24cm.
I hope this was helpful! I wish you have an amazing day!