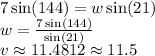Question

What the answer now answer only if now answer corry

Answer 1

Approximately 11.5 units.

Explanation:

We need to find the side opposite to ∠W. We are given the two angles ∠W and ∠X. We are also given that Side X is equal to 7. Therefore, we can use the Law of Sines.

Now, like last time, use the Law of Sines:

`(\sin(V))/(v)=(\sin(W))/(w)=(\sin(X))/(x)`

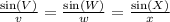
We can ignore the first term. Plug in 144 for ∠W, 21 for ∠X, and 7 for x.

`(\sin(144))/(w)=(\sin(21))/(7)`

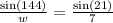
Cross multiply:

`7\sin(144)=w\sin(21)\\w=(7\sin(144))/(\sin(21)) \\v\approx11.4812\approx11.5`