Question

What the correct answer now

Answer 1

Area of the triangle WXY = 111.8 mm²

Explanation:

By applying Sine rule in the given triangle WXY,

`\frac{\text{SinW}}{\text{XY}}=\frac{\text{SinX}}{\text{WY}}=\frac{\text{SinY}}{\text{WX}}`

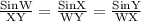
Since m∠W + m∠X + m∠Y = 180°

m∠W + 26° + 130° = 180°

m∠W = 180° - 156°

m∠W = 24°

`\frac{\text{Sin24}}{\text{XY}}=\frac{\text{Sin130}}{31}=\frac{\text{Sin26}}{\text{WX}}`

`\frac{\text{Sin24}}{\text{XY}}=\frac{\text{Sin130}}{31}`

XY =
`\frac{31* (\text{Sin24})}{\text{Sin130}}`

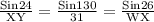
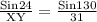
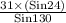
XY = 16.4597

≈ 16.4597 mm

Area of the triangle =
`(1)/(2)(\text{XY})(\text{WY})\text{SinY}`

=
`(1)/(2)(16.4597)(31)\text{Sin26}`

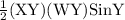
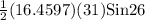
= 111.83 mm²

≈ 111.8 mm²

Therefore, area of the triangle WXY = 111.8 mm²