Answer:
Area of the triangle WXY = 111.8 mm²
Explanation:
By applying Sine rule in the given triangle WXY,
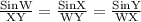
Since m∠W + m∠X + m∠Y = 180°
m∠W + 26° + 130° = 180°
m∠W = 180° - 156°
m∠W = 24°
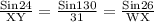
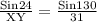
XY =

XY = 16.4597
≈ 16.4597 mm
Area of the triangle =
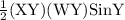
=
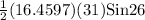
= 111.83 mm²
≈ 111.8 mm²
Therefore, area of the triangle WXY = 111.8 mm²