Question

1. an alloy contains zinc and copper in the ratio of 7:9 find weight of copper of it had 31.5 kgs of zinc.

2. compare the following ratios

i) 2:3 and 4:5
ii) 11:19 and 19:21
iii) ½ : ⅓ and ⅓ : ¼
iv ) 1⅕ : 1⅓ and ⅖ : 3/2

v) if a : b = 6:5 and b:c = 10:9, find a:c

vi) if x : y = ⅙:⅛ and y : z = ⅛: ⅒, find X : z

sorry many questions​

Answer 1

Explanation:

Question (1). An alloy contains zinc and copper in the ratio of 7 : 9.

If the weight of an alloy = x kgs

Then weight of copper =
`(9)/(7+9)* (x)`

=
`(9)/(16)* (x)`

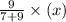
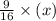
And the weight of zinc =
`(7)/(7+9)* (x)`

=
`(7)/(16)* (x)`

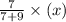
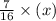
If the weight of zinc = 31.5 kg

31.5 =
`(7)/(16)* (x)`

x =
`(16* 31.5)/(7)`

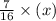
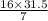
x = 72 kgs

Therefore, weight of copper =
`(9)/(16)* (72)`

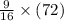
= 40.5 kgs

2). i). 2 : 3 =
`(2)/(3)`

4 : 5 =
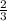
`(4)/(5)`

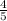
Now we will equalize the denominators of each fraction to compare the ratios.

`(2)/(3)* (5)/(5)` =
`(10)/(15)`

`(4)/(5)* (3)/(3)=(12)/(15)`

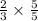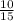
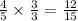
Since,
`(12)/(15)>(10)/(15)`

Therefore, 4 : 5 > 2 : 3

ii). 11 : 19 =
`(11)/(19)`

19 : 21 =
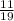
`(19)/(21)`

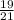
By equalizing denominators of the given fractions,

`(11)/(19)* (21)/(21)=(231)/(399)`

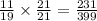
And
`(19)/(21)* (19)/(19)=(361)/(399)`

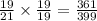
Since,
`(361)/(399)>(231)/(399)`

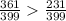
Therefore, 19 : 21 > 11 : 19

iii).
`(1)/(2):(1)/(3)=(1)/(2)* (3)/(1)`

`=(3)/(2)`

`(1)/(3):(1)/(4)=(1)/(3)* (4)/(1)`

=
`(4)/(3)`

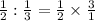
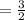
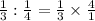
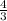
Now we equalize the denominators of the fractions,

`(3)/(2)* (3)/(3)=(9)/(6)`

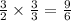
And
`(4)/(3)* (2)/(2)=(8)/(6)`

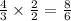
Since
`(9)/(6)>(8)/(6)`

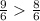
Therefore,
`(1)/(2):(1)/(3)>(1)/(3):(1)/(4)` will be the answer.

IV).
`1(1)/(5):1(1)/(3)=(6)/(5):(4)/(3)`

`=(6)/(5)* (3)/(4)`

`=(18)/(20)`

`=(9)/(10)`

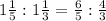
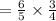
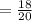
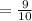
Similarly,
`(2)/(5):(3)/(2)=(2)/(5)* (2)/(3)`

`=(4)/(15)`

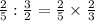
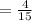
By equalizing the denominators,

`(9)/(10)* (30)/(30)=(270)/(300)`

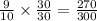
Similarly,
`(4)/(15)* (20)/(20)=(80)/(300)`

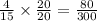
Since
`(270)/(300)>(80)/(300)`

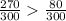
Therefore,
`1(1)/(5):1(1)/(3)>(2)/(5):(3)/(2)`

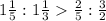
V). If a : b = 6 : 5

`(a)/(b)=(6)/(5)`

`=(6)/(5)* (2)/(2)`

`=(12)/(10)`

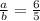
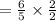
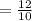
And b : c = 10 : 9

`(b)/(c)=(10)/(9)`

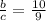
Since a : b = 12 : 10

And b : c = 10 : 9

Since b = 10 is common in both the ratios,

Therefore, combined form of the ratios will be,

a : b : c = 12 : 10 : 9