Question

An experiment involves 17 participants. From these, a group of 3 participants is to be tested under a special condition. How many groups of 3 participants can

be chosen, assuming that the order in which the participants are chosen is irrelevant?
​

Answer 1

Answer: 680

Explanation:

When order doesn't matter,then the number of combinations of choosing r things out of n =
`^nC_r=(n!)/(r!(n-r)!)`

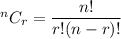
Given: Total participants = 17

From these, a group of 3 participants is to be tested under a special condition.

Number of groups of 3 participants chosen =
`^(17)C_3=(17!)/(3!(17-3)!)\`

`^(17)C_3=(17!)/(3!(17-3)!)\\\\=(17*16*15*14!)/(3*2*14!)\\\\=680`

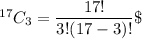
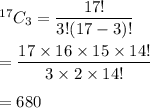
Hence, there are 680 groups of 3 participants can be chosen,.