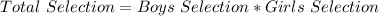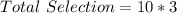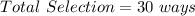Question

The four-member math team at Pecanridge Middle School is chosen from the math club, which has three girls and five boys. How many different teams made up of two girls and two boys could be chosen?

Answer 1

`Total\ Selection = 30\ ways`

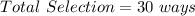
Explanation:

Given

Girls = 3

Boys = 5

Required

How many ways can 2 boys and girls be chosen?

The keyword in the question is chosen;

This implies combination and will be calculated as thus;

`Selection =\ ^nC_r = (n!)/((n-r)!r!)`

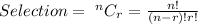
For Boys;

n = 5 and r = 2

`Selection =\ ^5C_2`

`Selection = (5!)/((5-2)!2!)`

`Selection = (5!)/(3!2!)`

`Selection = (5 * 4 * 3!)/(3!*2 * 1)`

`Selection = (20)/(2)`

`Selection = 10`

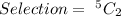
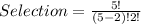
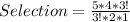
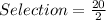
For Girls;

n = 3 and r = 2

`Selection =\ ^3C_2`

`Selection = (3!)/((3-2)!2!)`

`Selection = (3!)/(1!2!)`

`Selection = (3 * 2!)/(1 *2!)`

`Selection = (3)/(1)`

`Selection = 3`

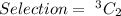
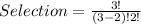
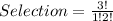
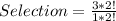
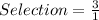
Total Selection is calculated as thus;

`Total\ Selection = Boys\ Selection * Girls\ Selection`

`Total\ Selection = 10 * 3`

`Total\ Selection = 30\ ways`