Question

*provide details with your answer if its NECESSARY. * What is the perimeter of this triangle?

Answer 1

27 units that’s the answer

Answer 2

27.9 units

Option B is the correct answer.

Explanation:

Finding the distance between the points A and B

A ( 3 , - 1 ) → ( x1 , y1 )

B ( 9 , - 5 )→ ( x2 , y2 )

Distance =
`\sqrt{ {(x2 - x1)}^(2) + {(y2 - y1)}^(2) }`

`= \sqrt{ {(9 - 3)}^(2) + {( - 5 - ( - 1)}^(2) }`

`= \sqrt{ {(9 - 3)}^(2) + {( - 5 + 1))}^(2) }`

`= \sqrt{ {6}^(2) +( - 4) ^(2) }`

`= √(36 + 16)`

`= √(52)`

`= 2 √(13)`

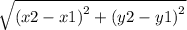
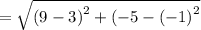
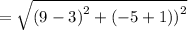
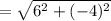
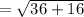
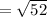
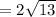
Finding the distance between the points B and C

B ( 9 , - 5 ) → ( x1 , y1 )

C ( 16 , - 2 )→ ( x2 , y2 )

Distance =
`\sqrt{ {(x2 - x1)}^(2) + {(y2 - y1)}^(2) }`

`= \sqrt{ {(16 - 9)}^(2) + { (- 2 - ( - 5))}^(2) }`

`= \sqrt{ {(16 - 9)}^(2) + { ( - 2 + 5)}^(2) }`

`= \sqrt{ {7}^(2) + {(3)}^(2) }`

`= √(49 + 9)`

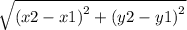
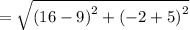
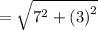
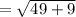
`= √(58)` units

Finding the distance between the points A and C

A ( 3 , - 1 )→ ( x1 , y1 )

C ( 16 , - 2 )→ ( x2 , y2 )

Distance =
`\sqrt{ {(x2 - x1)}^(2) + {(y2 - y1)}^(2) }`

`= \sqrt{ {(16 - 3)}^(2) + {( - 2 - ( - 1))}^(2) }`

`= \sqrt{ {(16 - 3)}^(2) + ( - 2 + 1) ^(2) }`

`= \sqrt{ {13}^(2) + ( { - 1)}^(2) }`

`= √(169 + 1)`

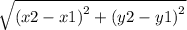
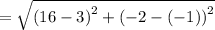
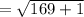
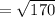`= √(170)` units

Now, let's find the perimeter:

Perimeter = AB + BC + AC

plug the values

`= 2 √(13) + √(58) + √(170)`

Calculate

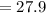`= 27.9` units

Hope this helps..

Best regards!!