Question

Which value of m will create a system of parallel lines with no solution? y=mx-6 8x-4y=12 A coordinate grid with one line labeled 8 x minus 4 y equals 12. The line passes through a point at (0, negative 3), (1, negative 1) and a point at (1.5, 0). -2 - 2

Answer 1

short answer is 2 or d

Explanation:

Answer 2

A system of parallel lines will be created where the two lines will never meet and have no common solution at a value of m = 2

Explanation:

The equation of the given line is 8·x - 4·y = 12

Which gives;

8·x- 12= 4·y

y = 2·x - 3

Given that the line passes through the points (0, -3) and (1, -1), we have;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

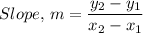
When (x₁, y₁) = (0. -3) and (x₂, y₂) = (1, -1), we have;

`Slope, \, m =((-1)-(-3))/(1-(0)) = 2`

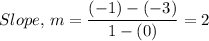
y - (-3) = 2×(x - 0)

y = 2·x - 3 which is the equation of the given line

For the lines 8·x - 4·y = 12, which is the sane as y = 2·x - 3 and the line y = m·x - 6 to have no solution, the slope of the two lines should be equal that is m = 2

Given that the line passes through the point (1.5, 0), we have;

y - 0 = 2×(x - 1.5)

y = 2·x - 3...................(1)

For the equation, y = m·x - 6, when m = 2, we have;

y = 2·x - 6..................(2)

Solving equations (1) and (2) gives;

2·x - 3 = 2·x - 6, which gives;

2·x - 2·x= - 3 - 6

0 = 9

Therefore, a system of parallel lines will be created where the two lines will never meet and have no common solution at a value of m = 2.