Question

A baby bird jumps from a tree branch and flutters to the ground. The function "f" models the bird's height (in meters) above the ground as a function of time (in seconds) after jumping. What is bird's height above the ground when it jumped.

Answer 1

It is (0,12) on the graph , if you are doing it on Khan Academy.

Explanation:

Just try it . se what happens. :))

Answer 2

The answer to this question will depend on the function f itself. Basically you will find the height in meters above the ground of the bird when it jumped when the time t=0s. This is substsitute every t in the function for a value of zero and that way you will get the bird's height at the time it jumped. If you were given a graph for this function, you can find the y-intercept of the graph and that will be the answer as well. The question could be written like this:

A baby bird jumps from a tree branch and flutters to the ground. The function "
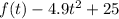`f(t)-4.9t^(2)+25`" models the bird's height (in meters) above the ground as a function of time (in seconds) after jumping. What is bird's height above the ground when it jumped.

Answer:

25m

Explanation:

Once your function is given, you can substitute t=0 since 0s is the time measured at the moment the bird jumped. So our function will be:

`f(0)=-4.9(0)^2+25`

`f(0)=25m`

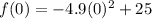
So the height of the bird above the ground when it jumped is 25m in this particular function.