Question

Please help me with this problem​

Answer 1

A

Explanation:

In standard form, an ellipse's major axis is indicated by the
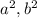`a^(2), b^(2)` terms like this:

`\frac{{(y-k)}^(2)}{a^(2)}+((x-h)^(2))/(b^(2)), a>b`

`\frac{{(x-h)}^(2)}{a^(2)}+((y-k)^(2))/(b^(2)), a>b`

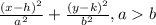
In the top equation, the vertical axis is primary and in the second the horizontal axis is primary. That's a bit more info than the question asked, but I thought it may be helpful to understand the answer.

Now, a co-vertex is the intersection point between an ellipse and its minor axis. On the graph of the ellipse, the
`b` is the distance from the center to where the ellipse intersects its minor axis, so our answer is A.

If a graphical representation would be helpful, I would take a look at the Math Warehouse article on the Equation of an Ellipse in Standard Form.