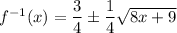Answer:
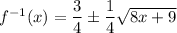
Explanation:
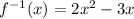
Change function notation to y.
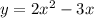
Switch x and y.
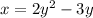
Solve for y.
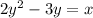
Complete the square on the left side. We must divide both sides by 2 to have y^2 as the leading term on the left side.
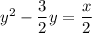
1/2 of 3/2 is 3/4. Square 3/4 to get 9/16.
Add 9/16 to both sides to complete the square.
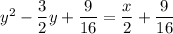
Find common denominator on right side.
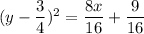
If X^2 = k, then
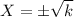
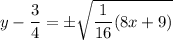
Simplify.
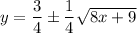
Back to function notation.