Question

A painter can paint a building in 15 days and a coworker can do the same job in 10 days. If the first painter starts and 3 days later the coworker joins in to help finish the job, how many days does it take to paint the building?

Answer 1

Answer: 7.8 days

Explanation:

Painter can get the job done in 15 days so gets
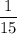`(1)/(15)` of the job done in 1 day.

Coworker can get the job done in 10 days so gets
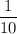`(1)/(10)` of the job done in 1 day.

Together, they get
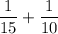`(1)/(15)+(1)/(10)` of the job done in 1 day.

Painter worked for 3 days so completed
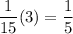`(1)/(15)(3)=(1)/(5)` of the job.

That leaves a remaining of
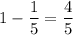`1-(1)/(5)=(4)/(5)` of the job to be completed.

Let x represent the number of days it will take them to work together.

Painter + Coworker = Together

`(1)/(15)(x)\quad +\quad (1)/(10)(x)\quad =\quad (4)/(5)`

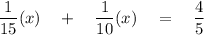
Multiply by 30 to eliminate the denominator:

`(1)/(15)(x)(30) +\ (1)/(10)(x)(30) = (4)/(5)(30)`

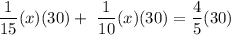
Simplify and solve for x:

2x + 3x = 24

5x = 24

`x=(24)/(5)`

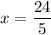
x = 4.8

Remember that Painter worked 3 days alone in addition to the 4.8 days they worked together.

So the total time to paint the building is 3 + 4.8 = 7.8