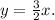The data in the table represents a direct variation, as the ratio
 remains constant
remains constant
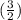 . The equation for the direct variation is
. The equation for the direct variation is
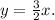
To determine whether the data represents direct variation or inverse variation, we can check if the ratio
 remains constant for all data points.
remains constant for all data points.
![\[ (y)/(x) = (9)/(6) = (12)/(8) = (18)/(12) = (30)/(20) = (3)/(2) \]](https://img.qammunity.org/2021/formulas/mathematics/college/s2als53khmpl9dy9qx905bcwg8qwsnuybk.png)
Since the ratio
 is constant (equal to
is constant (equal to
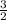 ), the data represents a direct variation. In a direct variation, the ratio of y to x is a constant value.
), the data represents a direct variation. In a direct variation, the ratio of y to x is a constant value.
Now, let's write the equation for direct variation. The general form is y = kx, where k is the constant of variation.
![\[ y = (3)/(2)x \]](https://img.qammunity.org/2021/formulas/mathematics/college/86c4u27ztffxgqgtv504a6qandwszzfgk9.png)
So, the equation that models the data in the table for direct variation is