Question

A 85.0kg man and a 65, 0kg woman are riding a Ferris wheel with a radius of 20.0m. What is the Ferris wheels tangential velocity if the net centripetal force on the woman is 115N

Answer 1

The Ferris wheel's tangential (linear) velocity if the net centripetal force on the woman is 115 N is 3.92 m/s.

Step-by-step explanation:

Let's use Newton's 2nd Law to help solve this problem.

• F = ma

The force acting on the Ferris wheel is the centripetal force, given in the problem:
`F_c=115 \ \text{N}`.

The mass "m" is the sum of the man and woman's masses:
`85+65= 150 \ \text{kg}`.

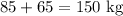The acceleration is the centripetal acceleration of the Ferris wheel:
`a_c=\displaystyle (v^2)/(r)`.

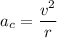Let's write an equation and solve for "v", the tangential (linear) acceleration.

• 
  `\displaystyle 115=m((v^2)/(r) )`
• 
  `\displaystyle 115 = (85+65)((v^2)/(20))`
• 
  `\displaystyle 115=150((v^2)/(20) )`
• 
  `.766667=\displaystyle((v^2)/(20) )`
• 
  `15.\overline{3}=v^2`
• 
  `v=3.9158`

The Ferris wheel's tangential velocity is 3.92 m/s.