Answer:
The missing side is
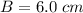
The missing angles are
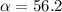 and
and

Explanation:
Given

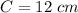
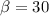
The implication of this question is to solve for the missing side and the two missing angles
Represent
Angle A with

Angle B with

Angle C with

Calculating B
This will be calculated using cosine formula as thus;
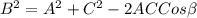
Substitute values for A, C and

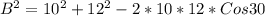
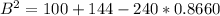
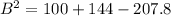
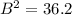
Take Square root of both sides
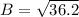
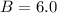 (Approximated)
(Approximated)
Calculating

This will be calculated using cosine formula as thus;
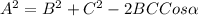
Substitute values for A, B and C
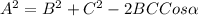
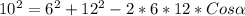
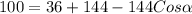
Collect Like Terms


Divide both sides by -144
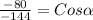

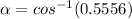
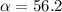 (Approximated)
(Approximated)
Calculating

This will be calculated using cosine formula as thus;
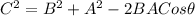
Substitute values for A, B and C
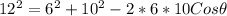
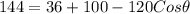
Collect Like Terms
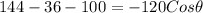
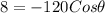
Divide both sides by -120
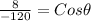

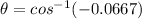
 (Approximated)
(Approximated)