Question

PLZZ HEPPP A line passes through (−1, 5) and (1, 3). Which answer is the equation of the line? x + 2y = 7 x + y = 4 x + 2y = 5 x + y = 2

Answer 1

B.

Explanation:

Again, to find the equation of the line, we need to find the slope and y-intercept. First, let's find the slope. Let (-1,5) be x₁ and y₁ respectively and (1,3) be x₂ and y₂, respectively. So:

`m=(y_2-y_1)/(x_2-x_1)=(3-5)/(1--1)=(-2)/(2)=-1`

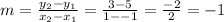
So the slope is -1.

Now, to find the y-intercept, we can use the point-slope form. I'm going to keep using (-1,5) as the coordinate. Thus:

`y-y_1=m(x-x_1)\\y-5=-1(x-(-1))\\y-5=-(x+1)\\y-5=-x-1\\y=-x+4`

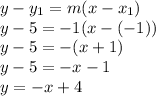
This is slope-intercept form. We want the answer to be in standard form, where:

`Ax+By=C`

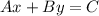
A, B, and C are integers (and, conventionally, A is positive).

Thus, we need to rearrange the terms:

`y=-x+4\\y+x=4\\x+y=4`

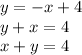
The answer is B.