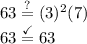Answer:
Length=Width=3
Height=7.
Explanation:
First, let's write some equations. So, we have an open box (with no lid) that has a square base. It has a height 4 units more of its width/length.
First, let's write the equation for the volume. The volume of a rectangular prism is:
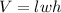
Recall that we have a square base. In other words, the length and width are exactly the same. Therefore, we can do the following substitution:
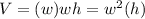
Now, recall that the height is four units more than the width/length. Therefore, we can make the following substitution:
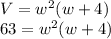
We can't really do anything with this. Let's next find the equation for the surface area.
So, we have 5 sides (not 6 because we have no lid). The bottom side is a square, so it's area is w^2. Since we have a square base, the remaining four sides will have an area w(w+4). In other words:
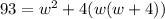
The left term represents the area of the square base. The right term represents the area of one of the rectangular sides, times sides meaning four sides. Simplify:
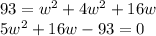
This seems solvable. Let's try it. Trying factoring by guessing and checking.
We can see that it is indeed factor-able. -15 and 31 are the numbers:
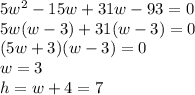
We ignore the other one because width cannot be negative.
So, the width/length is 3 and the height is 7. We can check this by plugging this into the volume formula: