Question

Please answer this question now

Answer 1

541.4 m²

Explanation:

Step 1: find m < V

V = 180 - (50+63) (sum of the angles in ∆)

V = 67

Step 2: find side length of XW using the law of sines

`(XW)/(sin(V)) = (XV)/(sin(W))`

Where,

V = 67°

W = 63°

XV = 37 m

XW

`(XW)/(sin(67)) = (37)/(sin(63))`

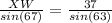
Multiply both sides by sin(67) to solve for XW

`(XW)/(sin(67))*sin(67) = (37)/(sin(63))*sin(67)`

`XW = (37*sin(67))/(sin(63))`

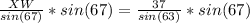
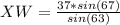
`XW = 38.2 m` (to nearest tenth)

Step 3: find the area using the formula, ½*XW*XV*sin(X)

area = ½*38.2*37*sin(50)

Area = 541.4 m² (rounded to the nearest tenth.