Question

How does the graph of g(x) = (x + 2)3 − 7 compare to the parent function of f(x) = x3? g(x) is shifted 2 units to the right and 7 units down. g(x) is shifted 7 units to the right and 2 units up. g(x) is shifted 2 units to the left and 7 units down. g(x) is shifted 7 units to the left and 2 units down

Answer 1

g(x) is shifted 2 units to the left and 7 units down.

Explanation:

I took it and got it correct.

Answer 2

Answer: g(x) is shifted 2 units to the left and 7 units down.

Explanation:

• The original function f(x) becomes f(x+c), if it is shifted c units to the left.
• The original function f(x) becomes f(x-c), if it is shifted c units to the right.
• Also, if it is shifted d units down, then the function becomes f(x)-d.
• If it is shifted d units up, then the function becomes f(x)+d.

Here, if we compare the graph of
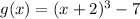`g(x) = (x + 2)^3 -7` compare to the parent function of
`f(x) = x^3`.

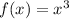We can observe that f(x) is shifted 2 units to the left and 7 units down.

So, the correct statement is "g(x) is shifted 2 units to the left and 7 units down".