Question

A 2 m tall, 0.5 m inside diameter tank is filled with water. A 10 cm hole is opened 0.75 m from the bottom of the tank. What is the velocity of the exiting water? Ignore all orificelosses.

Answer 1

4.75 m/s

Step-by-step explanation:

The computation of the velocity of the existing water is shown below:

Data provided in the question

Tall = 2 m

Inside diameter tank = 2m

Hole opened = 10 cm

Bottom of the tank = 0.75 m

Based on the above information, first we have to determine the height which is

= 2 - 0.75 - 0.10

= 2 - 0.85

= 1.15 m

We assume the following things

1. Compressible flow

2. Stream line followed

Now applied the Bernoulli equation to section 1 and 2

So we get

`(P_1)/(p_g) + (v_1^2)/(2g) + z_1 = (P_2)/(p_g) + (v_2^2)/(2g) + z_2`

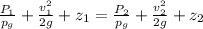
where,

P_1 = P_2 = hydrostatic

z_1 = 0

z_2 = h

Now

`(v_1^2)/(2g) + 0 = (v_2^2)/(2g) + h\\\\V_2 < < V_1 or V_2 = 0\\\\Therefore\ (v_1^2)/(2g) = h\\\\v_1^2 = 2gh\\\\ v_1 = √(2gh) \\\\v_1 = √(2* 9.8* 1.15)`

= 4.7476 m/sec

= 4.75 m/s