Question

An urn contains 5 white and 10 black balls. A fair die is rolled and that numberof balls are randomly chosen from the urn. What is the probability that all of theballs selected are white? What is the conditional probability that the die landed on3 if all the balls selected are white?

Answer 1

Explanation:

`A`- all of the chosen balls are white
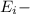`E_(i)-` result of the die roll is
`i, \quad i \in\{1,2,3,4,5,6\}`

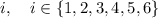
Probabilities:

since the die is fair:

`P\left(E_(i)\right)=(1)/(6) \quad \text { for } \quad i \in\{1,2,3,4,5,6\}`

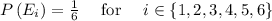
If the die rolls
`i` we choose a combination of
`i` balls, among 10 black and five white balls, therefore

\[ \begin{array}{c}

P\left(A \mid E_{1}\right)=\frac{\left(\begin{array}{c} 5 \\

1 \end{array}\right)}{\left(\begin{array}{c} 15 \\ 1 \end{array}\right)}=\frac{5}{15}=\frac{1}{3} \\ P\left(A \mid E_{2}\right)=\frac{\left(\begin{array}{c} 5 \\ 2 \end{array}\right)}{\left(\begin{array}{c} 15 \\ 2

\end{array}\right)}=\frac{10}{105}=\frac{2}{21} \\

P\left(A \mid E_{3}\right)=\frac{\left(\begin{array}{c} 5 \\ 3

\end{array}\right)}{\left(\begin{array}{c} 15 \\ 3

\end{array}\right)}=\frac{10}{455}=\frac{2}{91} \\

P\left(A \mid E_{4}\right)=\frac{\left(\begin{array}{c} 5 \\ 4

\end{array}\right)}{\left(\begin{array}{c} 15 \\ 4

\end{array}\right)}=\frac{1}{273} \\

P\left(A \mid E_{5}\right)=\frac{\left(\begin{array}{c} 5 \\ 5

\end{array}\right)}{\left(\begin{array}{c} 15 \\ 5

\end{array}\right)}=\frac{1}{3003} \\

P\left(A \mid E_{6}\right)=\frac{\left(\begin{array}{c} 5 \\ 6

\end{array}\right)}{\left(\begin{array}{c} 15 \\ 6

\end{array}\right)}=0

\end{array} \]