Answer:
The maximum displacement of the mass m₂
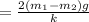
Step-by-step explanation:
Kinetic Energy (K) = 1/2mv²
Potential Energy (P) = mgh
Law of Conservation of energy states that total energy of the system remains constant.
i.e; Total energy before collision = Total energy after collision
This implies that: the gravitational potential energy lost by m₁ must be equal to sum of gravitational energy gained by m₂ and the elastic potential energy stored in the spring.
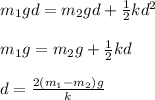
d = maximum displacement of the mass m₂