Question

Find the number c that satisfies the conclusion of the Mean Value Theorem on the given interval. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) f(x)

Answer 1

2.25

Explanation:

The computation of the number c that satisfied is shown below:

Given that

`f(x) = √(x)`

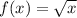
Interval = (0,9)

According to the Rolle's mean value theorem,

If f(x) is continuous in {a,b) and it is distinct also

And, f(a) ≠ f(b) so its existance should be at least one value

i.e

`f^i(c) = (f(b) - f(a))/(b -a )`

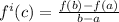
After this,

`f(x) = √(x) \\\\ f^i(x) = (1)/(2)x ^{(1)/(2) - 1} \\\\ = (1)/(2)x ^{(-1)/(2)`

`f^i(x) = \frac{1}{{2}√(x) } = f^i(c) = \frac{1}{{2}√(c) } \\\\\a = 0, f (a) = f(o) = √(0) = 0 \\\\\ b = 9 , f (b) = f(a) = √(9) = 3\\`

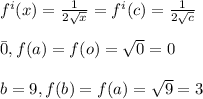
After this,

Put the values of a and b to the above equation

`f^i(c) = (f(b) - f(a))/(b - a) \\\\ \frac{1}{{2}√(c) } = (3 -0)/(9-0) \\\\ \frac{1}{\sqrt[2]{c} } = (3)/(9) \\\\ \frac{1}{\sqrt[2]{c} } = (1)/(3) \\\\ \sqrt[2]{c} = 3\\\\√(c) = (3)/(2) \\\\ c = (9)/(4)`

= 2.25