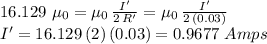Question

A conventional current of 3 A runs clockwise in a circular loop of wire in the plane, with center at the origin and with radius 0.093 m. Another circular loop of wire lies in the same plane, with its center at the origin and with radius 0.03 m. How much conventional current must run counterclockwise in this smaller loop in order for the magnetic field at the origin to be zero

Answer 1

The current in the small radius loop must be 0.9677 A

Step-by-step explanation:

Recall that the formula for the magnetic field at the center of a loop of radius R which runs a current I, is given by:

`B=\mu_0\,(I)/(2\,R)`

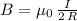
therefore for the first loop in the problem, that magnetic field strength is:

`B=\mu_0\,(I)/(2\,R) =\mu_0\,(3)/(2\,(0.093)) =16.129\,\mu_(0)\,`

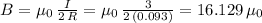
with the direction of the magnetic field towards the plane.

For the second smaller loop of wire, since the current goes counterclockwise, the magnetic field will be pointing coming out of the plane, and will subtract from the othe field. In order to the addition of these two magnetic fields to be zero, the magnitudes of them have to be equal, that is:

`16.129\,\,\mu_(0)=\mu_0\,(I')/(2\,R') =\mu_(0)\,(I')/(2\,(0.03)) \\I'=16.129\,(2)\,(0.03)=0.9677\,\,Amps`