Question

A magazine article states that the mean weight of one-year-old boys is the same as that of one-year-old girls. Does the confidence interval contradict this statement? The confidence interval this statement

Answer 1

Yes, the confidence interval contradict this statement.

Explanation:

The complete question is attached below.

The data provided is:

`n_(1)=318\\n_(2)=297\\\bar x_(1)=25\\\bar x_(2)=24.1\\s_(1)=3.6\\s_(2)=3.8`

Since the population standard deviations are not provided, we will use the t-confidence interval,

`CI=(\bar x_(1)-\bar x_(2))\pm t_{\alpha/2, (n_(1)+n_(2)-2)}\cdot s_(p)\cdot\sqrt{(1)/(n_(1))+(1)/(n_(2))}`

Compute the pooled standard deviation as follows:

`s_(p)=\sqrt{((n_(1)-1)s_(1)^(2)+(n_(2)-1)s_(2)^(2))/(n_(1)+n_(2)-2)}=\sqrt{((318-1)(3.6)^(2)+(297-1)(3.8)^(2))/(318+297-2)}=2.9723`

The critical value is:

`t_{\alpha/2, (n_(1)+n_(2)-2)}=t_(0.05/2, (318+297-2))=t_(0.025, 613)=1.962`

*Use a t-table.

The 95% confidence interval is:

`CI=(\bar x_(1)-\bar x_(2))\pm t_{\alpha/2, (n_(1)+n_(2)-2)}\cdot s_(p)\cdot\sqrt{(1)/(n_(1))+(1)/(n_(2))}`

`=(25-24.1)\pm 1.962* 2.9723* \sqrt{(1)/(318)+(1)/(297)}\\\\=0.90\pm 0.471\\\\=(0.429, 1.371)\\\\\approx (0.43, 1.37)`

The 95% confidence interval for the difference between the mean weights is (0.43, 1.37).

To test the magazine's claim the hypothesis can be defined as follows:

H₀: There is no difference between the mean weight of 1-year old boys and girls, i.e.
`\mu_(1)-\mu_(2)=0`.

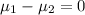Hₐ: There is a significant difference between the mean weight of 1-year old boys and girls, i.e.
`\mu_(1)-\mu_(2)\\eq 0`.

Decision rule:

If the confidence interval does not consists of the null value, i.e. 0, the null hypothesis will be rejected.

The 95% confidence interval for the difference between the mean weights does not consists the value 0.

Thus, the null hypothesis will be rejected.

Conclusion:

There is a significant difference between the mean weight of 1-year old boys and 1-year old girls.