Answer:
Mean = 2.14
Standard deviation = 2.40
Explanation:
The calculation of mean and standard deviation is shown below:-
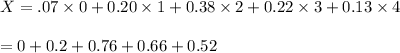
= 2.14
So, the mean is 2.14
Now, For computing the standard deviation first we need to find out the variance which is shown below:-
Variance is
![Var(X) = P(X^2) - [P(X)]^2\\\\ P(X^2) = .07* (0^2) + .20* (0^1) + .38* (0^2) + .22* (0^3) +0.13* (0^4)](https://img.qammunity.org/2021/formulas/mathematics/high-school/sq6yntorznlzz21uqk7bjytf2j08bz0bea.png)
After solving the above equation we will get
= 5.78
Now, the standard deviation is
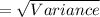
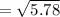
= 2.404163056
or
= 2.40