Answer:
The wave takes 0.132 seconds to travel from one end of the string to the other.
Step-by-step explanation:
The velocity of a transversal wave (
 ) travelling through a string pulled on both ends is determined by this formula:
) travelling through a string pulled on both ends is determined by this formula:
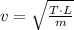
Where:
 - Tension, measured in newtons.
- Tension, measured in newtons.
 - Length of the string, measured in meters.
- Length of the string, measured in meters.
 - Mass of the string, measured in meters.
- Mass of the string, measured in meters.
Given that
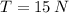 ,
,
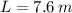 and
and
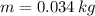 , the velocity of the tranversal wave is:
, the velocity of the tranversal wave is:
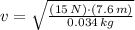
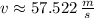
Since speed of transversal waves through material are constant, the time required (
 ) to travel from one end of the string to the other is described by the following kinematic equation:
) to travel from one end of the string to the other is described by the following kinematic equation:
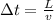
If
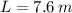 and
and
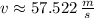 , then:
, then:
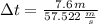
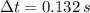
The wave takes 0.132 seconds to travel from one end of the string to the other.