Question

If the voltage amplitude across an 8.50-nF capacitor is equal to 12.0 V when the current amplitude through it is 3.33 mA, the frequency is closest to:

Answer 1

5.19 x 10³Hz

Step-by-step explanation:

The capacitive reactance,
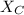`X_(C)`, which is the opposition given to the flow of current through the capacitor is given by;

`X_C = (1)/(2\pi fC )`

Where;

f = frequency of the signal through the capacitor

C = capacitance of the capacitor.

Also, from Ohm's law, the voltage(V) across the capacitor is given by the product of current(I) and the capacitive reactance. i.e;

V = I x
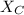`X_(C)` [Substitute the value of

=> V = I x
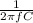`(1)/(2\pi fC)` [Make f the subject of the formula]

=> f =
`(I)/(2\pi VC)` ---------------------(i)

From the question;

I = 3.33mA = 0.00333A

C = 8.50nF = 8.50 x 10⁻⁹F

V = 12.0V

Substitute these values into equation (i) as follows;

f =
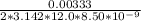`(0.00333)/(2 * 3.142 * 12.0 * 8.50 * 10^(-9))` [Taking
`\pi` = 3.142]

f = 5.19 x 10³Hz

Therefore, the frequency is closest to f = 5.19 x 10³Hz