Answer: E(X) = 4
V(X) =
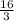
Step-by-step explanation: An uniform distribution is a random variable X restricted to a finite interval [a,b] and has a constant function f(x) over this interval, i.e., the function is of form:
f(x) =
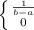
The mean or expectation of an unifrom distribution is:
E(X) =
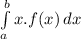
For the density function in interval [0,8], expectation value is:
E(X) =
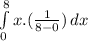
E(X) =
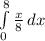
E(X) =
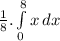
E(X) =
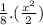
E(X) =
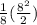
E(X) = 4
Variance of a probability distribution can be written as:
V(X) =
![E(X^(2)) - [E(X)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/74mvm0au1mq2yezx2dc091r7xgz47bdx02.png)
For uniform distribution in interval [0,8]:
V(X) =
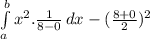
V(X) =
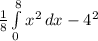
V(X) =
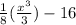
V(X) =
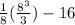
V(X) =
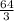 - 16
- 16
V(X) =
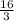
The mean and variance are 4 and 16/3, respectively