Answer:
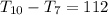
Explanation:
Given
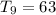
Required
Find
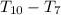
From the question, we have that:
Each sequence = 2 * Previous sequence + 1;
i.e.

Considering the 9th sequence;
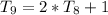 ------ Equation 1
------ Equation 1
Considering the 8th sequence;

Substitute
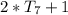 for
for
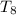 in equation 1
in equation 1
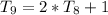 becomes
becomes
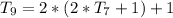
Open bracket

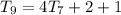
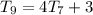
Substitute 63 for

Subtract 3 from both sides
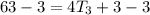
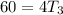
Divide both sides by 4

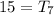
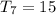
Considering
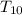
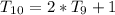
Substitute 63 for
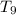

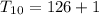
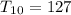
Calculating
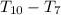
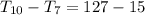
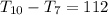
Hence, the 10th - 7th number is 112