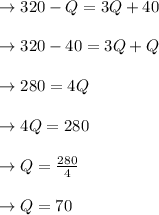Question

A​ monopoly's cost function is CQ and its the demand for its product is pQ where Q is​ output, p is​ price, and C is the total cost of production. Determine the profit-maximizingLOADING... price and output for a monopoly.

Answer 1

The answer is "70 units".

Step-by-step explanation:

In the given question some equation is missing which can be defined as follows:

`C = 1.5Q^2+40Q\\\\P=320-0.5Q`

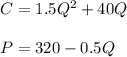
Monopolistic functions are used where Marginal Profit = Marginal Cost where marginal revenue and marginal cost stand for the MR and MC.

Finding the value of MR :

`\ MR = (\partial TR)/(\partial Q) \\\\`

`= (\partial PQ)/(\partial Q) \\\\= (\partial (320-0.5Q)Q)/(\partial Q)`

`= (\partial (320Q -0.5Q^2))/(\partial Q)\\\\ = (\partial Q (320 -0.5Q))/(\partial Q)\\\\ \ by \ solving \ we \ get \\\\ = 320 - Q...(1)`

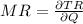
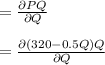
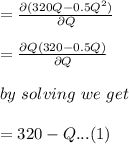
Calculating the value of the MC:

`MC = (\partial TC)/(\partial Q) \\`

`=(\partial (1.5Q^2 + 40Q))/(\partial Q) \\\\=(\partial Q (1.5Q + 40))/(\partial Q)\\\\ \ by \ solve \ value \\\\ = 3Q + 40....(2)`

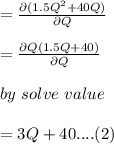
compare the above equation (i) and (ii):

`\to 320 -Q = 3Q+40\\\\\to 320 -40 = 3Q+ Q\\\\\to 280 = 4Q\\\\\to 4Q =280 \\\\\to Q= (280)/(4)\\\\\to Q= 70 \\`